Since I have been looking (again) at Reaction-Diffusion and Grid simulations, I was pointed to the www.shadertoy.com community with its incredible WebGL simulations.
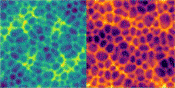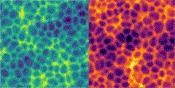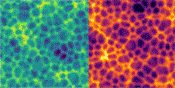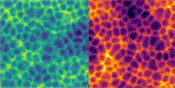
The first simulation on the ShaderToy platform that really struck me was this 'Cool Accident' sim by the CS-artist Wyatt, which has the 'dynamic foam' vibe that I have in mind. (But with no currents between the bubbles.)
If you aren't familiar with Shadertoy, you should definitely check them out. You can run them yourself in your browser, best in Google's Chrome and you need to activate WebGL.
If you aren't familiar with Shadertoy, you should definitely check them out. You can run them yourself in your browser, best in Google's Chrome and you need to activate WebGL.
An other amazing computer-scientist on the Shadertoy platform is Michael Moroz who made this dynamic 'Pilot Wave System' Voronoi simulation, that comes close to my Dynamic Foam.
I reached out to them and asked to add a Half-Edge structure to his sim, that distributes the currents between the cells, transporting energy; so the dynamics of pressure going from left to right, that you see in the animated gif and which are done manually, would all happen automatically.
Note, Half-Edges are way to add graphs to the edges of a Mesh.
Now Michael has made some additions to his simulations, that are a big leap forward!
Based on Wyatt Flanders' GLS shader research
(Use Chrome to activate Shaders)