Simulated by Václav Šmilauer with his program WOO-DEM:
Ref.: Neighbor list collision-driven molecular dynamics simulation for nonspherical hard particles. - II. Applications to ellipses and ellipsoids. by Aleksandar Donev, Salvatore Torquato, Frank H. Stillinger
Original movie: http://flux.doxos.eu/temp/ell2d-equal.avi (80 Mb)
Box-simulation: http://flux.doxos.eu/temp/ell2d-grp-mesh.zip
Unpack and open with Paraview, import the whole group-package, press apply, and play …
you can color them by velocity, angular velocity, use filters to show traces and whatnot.
The ellipsoids of different sizes in this case are rendered as icosahedra.
-
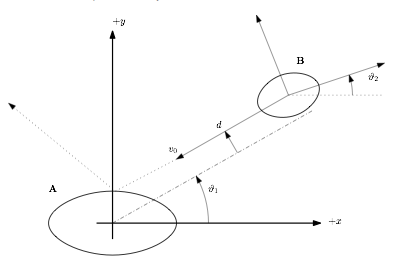
Before this group-simulation some individual 0ne on 0ne simulations were done to test the slipperiness (frictionless) of the 0vals and to see how they deflect.
0val 'A' is set and 'B' comes flying in. The results are shown in the graphs below.
Left graph: the angle of 'B' changes - Right graph: 'B' has only one value.
'B' is coming along (+X) with differing (d); for every (d), there are three different (V2): 0, 0.1 and 0.2 radians - the lines coming from the right split in 3 parts depending on (V2).
Hitting a slippery floor; left graph, with (V1) varying; the two right tables (close-up): with density varying (changing density changes both mass and inertia); they both depend linearly on density, therefore have the same proportion and there is no difference in angle, but the angle is stretched out from (V) towards (\__/) and thus adding more linearity.
-
Next up is doing some testing with all the possible settings and see if steady vortex-structures-patterns would show in this sort of medium, by using different ellipsoidal shapes, velocities and densities, as mentioned in Spiraling Figure 8.