Spiraling Figure 8

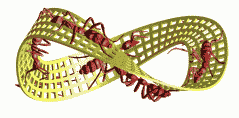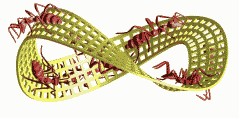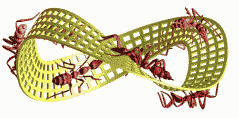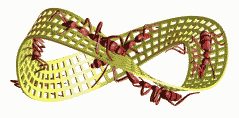
A short animated-gif of the upwards spiraling figure 8 particle, from the older high res Screencast-movie that I mention in 'About Me' on the side (movie - 40Mb) ... and what this project is about. 

Similar to Professor Oscar Velasco Fuentes' knotted filamentary-vortex:

The final goal is to get this action 'naturally' going within a gas made out of frictionless (ellipsoidal) particles, wherein these of loops automatically would emerge thanks to the right destiny and velocity of the particles that make up the medium. Check the iPhone physics-app 'Liquid' to get an impression of such a gas: https://itunes.apple.com/en/app/liquid-dynamics/id417814216?mt=8. When you adjust the settings you get a medium where continuously semi-vortices pop up (see pic.):

Note: If you haven’t got an iPhone you could check this Java-applet made by Grant Kot: http://grantkot.com/MPM/Liquid.html The iPhone ‘Liquid' App is based on this Java-applet and is roughly the same. In the image below are the settings (upper line-table only blue-green) to get the similar semi-vortices that quickly come an go in and out of existence (note on the iPhone app it’s slightly more intenser and more pronounced), and you need to play with it for a couple of seconds and wait a little to let the gas stabilize ...

... but these semi-vortices are unstable and come and go into existence, so that's why the idea surfaced to use slippery 0val-bodies instead of the 'classic' spherical point-particles; and because these 0val-particles interact in a unique way, with the path that redirects them again along their central-axis, they might a that extra ingredient to the medium, whereby some of these semi-vortices are replaced by vortices that are stable, and take on a steady / solid form within the medium, a bit like how these kids form a closed loop (Ouroboros):

Chirality External vs. Internal

In the world of Nano-technology and Self-Propelled Particles (SPP) it is said that Chirality (handedness) is needed for vortex-formations to occur. True, but chirality could also happen due to an external factor, differences in pressure (density fluctuations) within the medium in reference to a perfectly symmetric forward moving SPP.

Milling Ants - Koi Fish

An ant-mill is an observed phenomenon in which a group of army ants separated from the main foraging party lose the pheromone track and begin to follow one another, forming a continuously rotating circle. The ants will eventually die of exhaustion. This has been reproduced in laboratories and the behaviour has also been produced in ant colony simulations. This phenomenon is a side effect of the self-organizing structure of ant colonies. Each ant follows the ant in front of it, and this will work until something goes wrong and an ant mill forms.

http://en.wikipedia.org/wiki/Ant_mill

A unique case of circular milling in ants, considered in relation to trail following and the general problem of orientation. by Schneirla, T. C. (3.8 Mb)

Figure 800 - MC Escher's Moebius Ring with Ants (ref.)

Vortex Loops, Helical Spring and Hair Vortex

Vorticity in shearing plasma layers as strings of identical helix units smoothly joined at their junctions. We present scaling versions of vortex stretching, breaking and reconnection at high Reynolds number breeding chiral vortex loops as in phase slippage events in superfluids. 

Helix String Model For Turbulent Vorticity and Cavitation in Shearing Arc Plasma by Geert C. Dijkhuis

Here we report the creation of isolated trefoil vortex knots and pairs of linked vortex rings in water using a new method of accelerating specially shaped hydrofoils.

Creation and dynamics of knotted vortices by Dustin Kleckner & William T. M. Irvine

We start by analyzing the origin of chirality in simple systems such as the helical spring and hair vortex.

Emerging chirality in nanoscience by Yong Wang, Jun Xu, Yawen Wanga and Hongyu Chen

 

Laser-induced micro-scale vortex rings have been generated on vaporising tantalum surface, and their reconnection was studied in the presence of shock waves on the nanosecond time scale. A rich spectrum of the ring structures was obtained, some of which have been observed for the first time.

Observation of Laser-Induced Microscale Vortex Ring Interactions on Vaporizing Metal Surface by S. Lugomer

Braids of vortex filaments generated by laser on metal surface by S. Lugomer

Using the multipulse laser-matter interaction with the Co-coated surface, a one-dimensional high-density vortex-filament array has been created. Increasing the number of pulses, the oscillatory strain field causes the cascade of the shape transformations into structures of increasing topological complexity: vortex filaments into ribbons, into ribbon helicoids and tubular-ribbon helicoids, and then into short ribbon structures with the complex Scherk surface being identified.

Generation of ribbons, helicoids, and complex Scherk surfaces in laser-matter interactions by Lugomer S., Fukumoto Y.