Acute Angle Detection : Geometrical, Mechanical or Kernel

The corners in our Dynamic Foam are like gates in an electronic circuit or valves in a 'classical' flow system. When the angle is Acute, smaller then 90 degrees (< 90°), the flow is cut-off. 

This is the main rule that regulates our system and generates structure (closed-knots) like Leonardo's bridge.

So in our Foam, Voronoi-mesh, we need to detect the Acute angles ... 

... were the angles pass the 90° mark:

I have been investigating 3 methods to solve our Acute Angle Detection:

I. Geometric

There are 3 geometrical methods to calculate the angles when you have the 3 reference points, you can check it all here: https://www.wikihow.com/Calculate-Angles

https://www.shadertoy.com/view/McyBzd

II. Mechanical

The mechanical method uses a perpendicular placed marker with:

length = distance from pivot-point.

You can test it with the Shadertoy example:

https://www.shadertoy.com/view/l3ccRN

Instead of a perpendicular-stripe you can also use a circle and do a boolean cut ...

... and for 3D use a Sphere with a plane to do the cut.

Technically in the program we can:

A. Implement the calculation at each edge-end.

B. Do the calculation once and use it as a stencil to 'print' it at each edge-end.

III. Kernel

A pixel 'kernel' that does a 'numbers' match-check.

IXIXIXIXIXI

IXIXIOIXIXI

IXIOIXIOIXI

IOIXIXIXIOI

IXIXIXIXIXI

Although I haven't throught this through yet. 😁

To be continued ...

Acuteness Cells

 A new ’slightly’ different approach that might be a lot easier to process the Dynamic Foam:

Instead of doing a search along the edges, where the acute angles (sharp < 90°) are the regulators ... we might get the same result by calculating the acute angles and ‘mark' the cells. Similar to Conways Game of Life.

The idea is that a tree search is equivalent to counting the surrounding cells, in both cases the same 'effect of the sharp corners’ in the foam is sensed and applied.

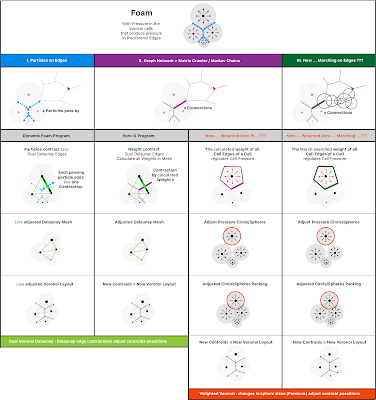
I. Previous models : Monte Carlo - and Local Edge Search

• Find Sharp-angels and mark the corners.

• Unique tree-search for each edge to define the Weight of each cell edge.

• Sum of all weights = > New Pressure.

• Balance out cells based on their new pressures and draw new Voronoi-Layout, with Power-Voronoi-tracking-cells*.

--

II. Future model : Acute Angles Counting / Sub Cells

• Detect Acute Angles

• Acuteness : Count Acute-angels per cell (0, 1, 2, 3)

• Color the whole cells depending on the acuteness value.

• Sum of all marked adjacent Sub-cells => New Pressure.

• Balance out cells based on their new pressures.

Like in Game of Live.

————

Shadertoy tests:

https://www.shadertoy.com/view/lfyfW1

• Sharp acute angles (<90°) are marked white.

• Based on N° of interior acute angles (1, 2, 3) the Voronoi cells change light yellow to dark orange.

• Blue Voronoi cells have no acute angles.

https://www.shadertoy.com/view/l3KyWd

Voronoi Cell Volume is regulated by number of 'adjacent' acute angles.

• Acuteness = acute angles (<90°) per Cell

• Cell Volume is regulated by Acutess: (0,1) increase <-> (2,3) decrease

• Cell color = Acuteness: 0 = White, 1= Blue, 2 = Red, 3 = Black

The relation to GoL is that in GoL we count the 'living' adjacent cells to define if a cell lives (increases) or dies (decreases). Here we count the number of acute-angles ‘around’ each cell, 

There are only 4 ‘acuteness’ levels possible: 0,1,2,3

When it's (0,1) the Volume of the cell increase / lives <-> (2,3) the cell decrease / dies. 

Like in GoL cells ‘live’ or ‘die’ depending on the organisation of its neigibours.

There's a ‘physical’ and a 'mental' part to this:

• Physical: circular-particles that can increase or decrease, and push each other away. The centers of these circular-particles are used as the Centroids of the Voronoi mesh on top of it. You can see cicular they are light transparent black.

• Mental: On top of the physical circular-particles is a Voronoi-mesh, that uses the centers of those circular-particles as centroid. Next for each Voronoi-cell we calculate the number of acute angles, and use these values to color the cells. We also feed this result to the 'physical' circular-particles, so they know how much they need to increase or decrease. Noter, we set an upper and lower bound, otherwise the sim explodes.

Result: The physical circular-particles change in size. -> They pushed each other. -> New Voronoi layout. -> New acuteness values for the cells. -> The physical circular-particles change in size -> Et c’est parti! -> C’est la vie! 😀

PS Blue noise distribution of the particles is for a ‘natural’ random distribution at the start, instead of Poison distribution. If we use for instance an symmetric array that gives us all clean tiled Voronoi cells with zero acute angles, then they all would decrease into a hole, it would be like starting GoL off with a block of black cells that all die.

--

The plan is now to use Voronoi-Tracking and introduce:

*Power-Voronoi-tracking-cells

The idea to adjust 'relatively' the Voronoi-particle-tracking pixels (texels) 

related to the Volume value of the particles to adjust 

the size of the tracking Voronoi Cells.

To be continued ...

Currents in the Edges Table

Overview table with the different approaches to solve the Dynamic Foam with Currents in the edges: Dynamic Foam and VoroX with a Dual Voronoi-Delaunay mesh, and also the suggestions for a new version with Weighted Voronoi, and a marching method to search along the edges.

The top layer has 3 methods to search the pressure distribution in the edges of the Voronoi Mesh, but it doesn’t change the Voronoi Mesh physically. 

I. Particles move ‘live’ along the Edges, this is used in the Dynamic Foam program made by Nick McDo: https://github.com/weigert/DynamicFoam/wiki/System-Dynamics

II. Use a search in the Geomatric matrix using Markov Chains like how Googles Page Rank works, this used in VoroX made by Benoît L.t: https://github.com/blegat/VoroX.jl

III. This is a new suggestion to use short local search by marching the edges and being blocked when running into a sharp angle.

This layer is about finding out the weight of each edge.

——

B. This next layers are how we apply the results from A to the mesh(es) and physically change the Voronoi (and Delaunay) Mesh and get a new Voronoi lay-out. With two columns:

Green: Dual Voronoi-Delaunay mesh: particles or weights on the Voronoi Mesh makes it’s dual-Delaunay edges contract, and shifting the centroids of the Voronoi Cells.

Orange: Weighted Voronoi: the total weights of a the Edges of a Voronoi cell change it’s Sphere size (pressure) and the Spere-packing changes due to each Spere new size.

——

Some diagrams regarding a Marching model.

A couple of short walks done in the direction of each connected edge to measure the weight of each edge.